Level: Medium project
GitHub Repository: https://github.com/JaumeAlbardaner/setSolver
What is "Set"?
Set is a fast-paced card game based on pattern recognition, where players race to identify sets of cards that share or differ across multiple attributes. The game is designed for 1 or more players and is known for its simplicity and depth of strategy, appealing to both casual and competitive players.

Deck
Set is a card game that consists of a total of 81 cards.
These cards contain the following:
- Shapes: Shapes of type Capsule (c), Romb (r), Wave (w).
- Filling: Shapes can be Light (l, no filling), Gradient (g, 50% filling), Dark (d, completely filled).
- Color: Shapes can take colors Green (g), Violet (v) or Red (r).
- Number: There can be 1, 2 or 3 shapes per card.
How is it played?
- Setup: Twelve cards are laid face-up in a grid.
- Finding a Set: Players race to find a set of three cards that meet the set criteria (either all the same or all different for each attribute). There are no turns; the first player to spot a set calls out "Set!" and points to the cards.
- Validation and Replacement: If the set is correct, the three cards are removed and replaced with new ones from the deck. If incorrect, the player must wait before calling another set.
- End of Game: The game continues until the deck is depleted and no more sets can be found. The player with the most sets wins.
It may also happen that with all twelve cards laid down there is no feasible combination of cards to be made.
The likeliness of this scenario happening is low, but not zero.
What is "Set Solver"?
Set Solver is a project that aims to solve the game of Set, mostly aimed to assure the player that there are no more sets to be found in the current layout of cards.
As seen in the previous explanation, there are two main technologies at work:
- Card recognition, to recognize each card and differentiate them from the others
- Logic, to ensure the constraints are respected.
To mimic human behavior, these two technologies have been approached with the use of YOLOv8 and a SAT-solver.
Card recognition
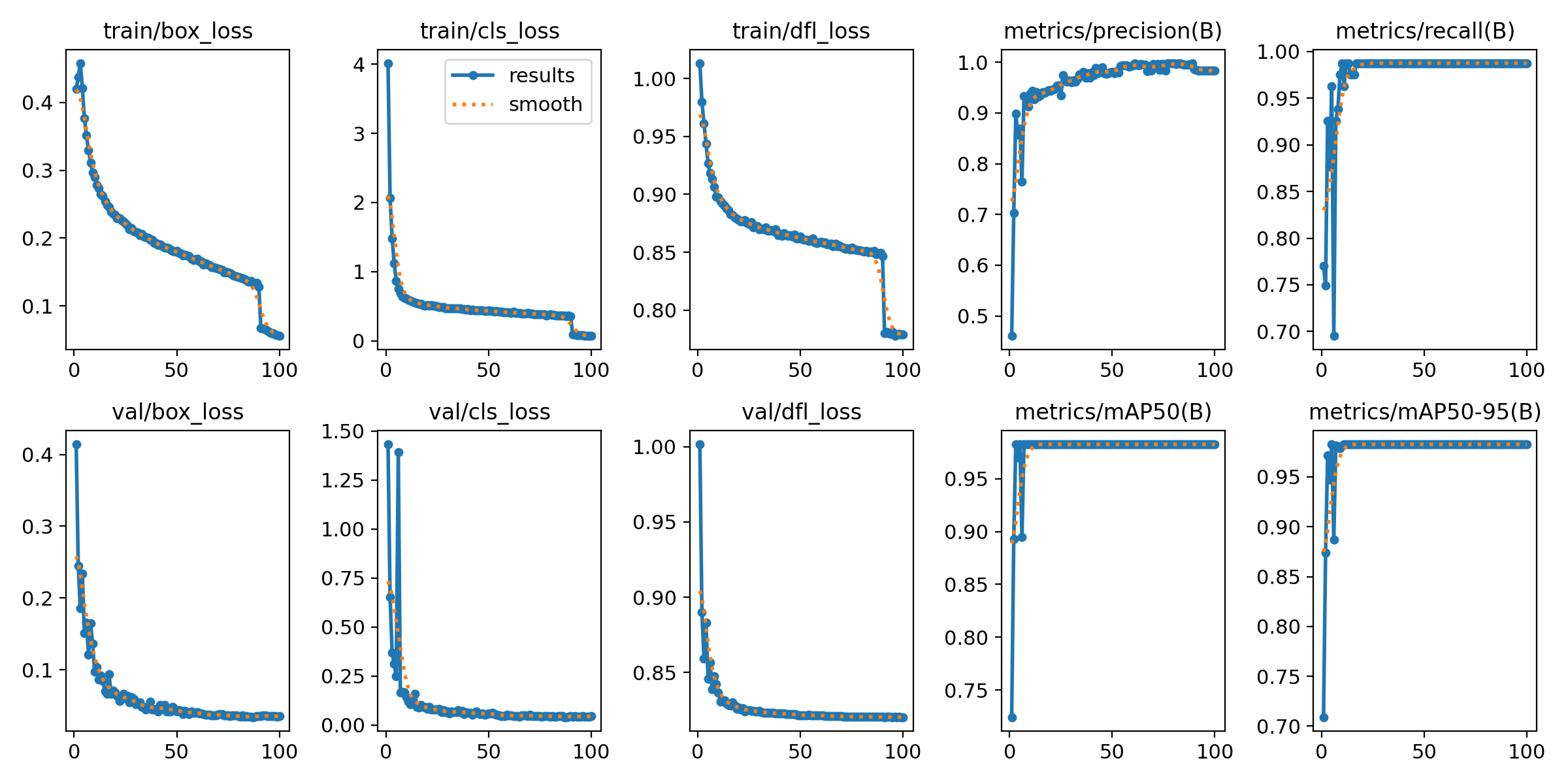
To train a YOLO model to recognize images, one usually needs thousands of images per class to be trained. Since I'm lazy I only took one picture of each card and added virtual noise to it later. Although it's not as robust, it saves a lot of time taking photos and labeling (mostly because we have 81 classes in this case).
The procedure to train the YOLO model was the following:
- Take pictures of all the cards on a black background.

- Run a segmentation algorithm to remove the parts of the image that don't belong to the card.

- With some randomization (translation/rotation/perspective transform), place the image of the card on top of another image (to act as noise) and write down its bounding box in a .txt file (YOLO standard).

(The rage comics were most of my already-downloaded resources, any other images are also accepted as noise.)
- Train the YOLO NN.
Logic
Since there are some constraints to be fulfilled, we must ensure that the selection of cards satisfies these conditions. Hence why I decided to use a SAT-solver.
A SAT solver is a software tool used to determine whether a given Boolean formula can be satisfied, meaning if there exists an assignment of true or false values to variables that makes the entire formula evaluate to true.
In this SAT problem, I've made the first N variables correspond to the "picking" of a card 1..N, meaning that if the variable is true, that card is one of the 3 cards that make a set.
After this, 12 boolean variables follow with the properties of each variable (4 properties * 3 possibilities = 12 boolean literals). The order of these variables is the following:
- (Shape) c r w
- (Filling) l g d
- (Color) g r v
- (Number) 1 2 3
To talk in the context of the SAT solver, the following clauses have to be applied:
- Exactly 3 cards must be selected.
Most solvers already implement the "exactly" restriction with the iterative use of atLeast and atMost. In the case of the Kotlin library used, it is called using solver.addExactly(new VecInt(variableArray), requiredTrue);
- If a card is selected, its properties must be fulfilled. E.g. in a card with properties 3 4 8 10 this would be set as follows:
x_1 → (3 ∧ 4 ∧ 8 ∧ 10)
(-x_1 ∨ 3) ∧ (-x_1 ∨ 4) ∧ (-x_1 ∨ 8) ∧ (-x_1 ∨ 10)
- A property can only be fulfilled if a card with said property is chosen. E.g. property 3 is present in cards
x_1,x_4,x_{12},x_9:
x_1 → (x_1 ∨ x_4 ∨ x_{12} ∨ x_9)
-x_1 ∨ x_1 ∨ x_4 ∨ x_{12} ∨ x_9
- There can't be a property with 2 different values (it must be either all the same or all different). For property with variables 3, 4, and 5.
(3 ∨ 4 ∨ 5) ∧ (3 ∨ -4 ∨ -5) ∧ (-3 ∨ 4 ∨ -5) ∧ (-3 ∨ -4 ∨ 5)
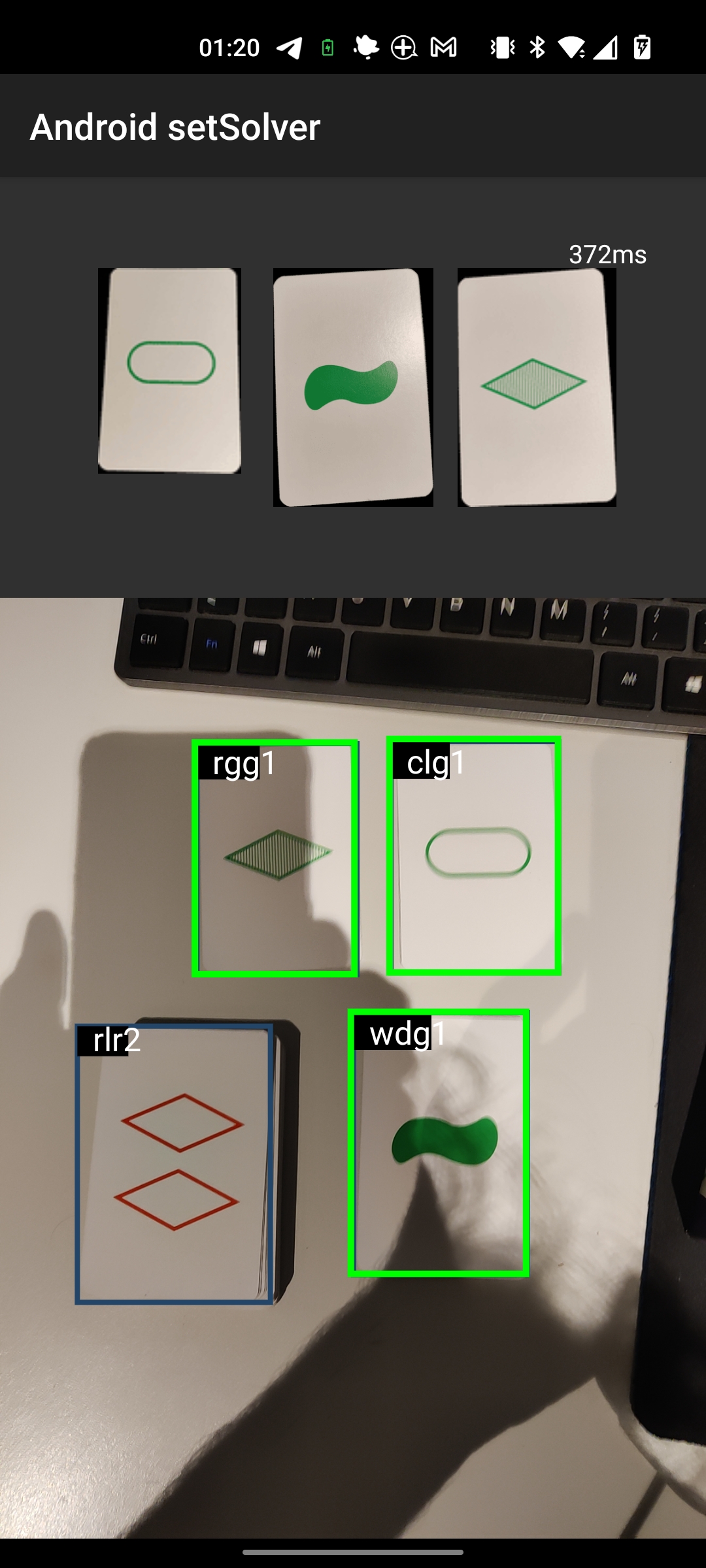
Resulting app
Combining the object detection together with the SAT-solver logic, the following result is achieved:
Images:

Videos:
