Level: Small project
GitHub Repository: https://github.com/JaumeAlbardaner/churro.c
What is "Churro.c"?
Churro.c is the spaniard-ization of the Donut.c program.What is "Donut.c"?
Donut.c is a doughnut-shaped code snippet written in C by Andy Sloane back in 2006 (code can be found in his website: https://www.a1k0n.net/2006/09/15/obfuscated-c-donut.html). Not only is the code shaped as a doughnut, but if compiled and executed it also outputs a doughnut in the terminal. A spinning one at that.
k;double sin()
,cos();main(){float A=
0,B=0,i,j,z[1760];char b[
1760];printf("\x1b[2J");for(;;
){memset(b,32,1760);memset(z,0,7040)
;for(j=0;6.28>j;j+=0.07)for(i=0;6.28
>i;i+=0.02){float c=sin(i),d=cos(j),e=
sin(A),f=sin(j),g=cos(A),h=d+2,D=1/(c*
h*e+f*g+5),l=cos (i),m=cos(B),n=s\
in(B),t=c*h*g-f* e;int x=40+30*D*
(l*h*m-t*n),y= 12+15*D*(l*h*n
+t*m),o=x+80*y, N=8*((f*e-c*d*g
)*m-c*d*e-f*g-l *d*n);if(22>y&&
y>0&&x>0&&80>x&&D>z[o]){z[o]=D;;;b[o]=
".,-~:;=!*#$@"[N>0?N:0];}}/*#****!!-*/
printf("\x1b[H");for(k=0;1761>k;k++)
putchar(k%80?b[k]:10);A+=0.04;B+=
0.02;}}/*****####*******!!=;:~
~::==!!!**********!!!==::-
.,~~;;;========;;;:~-.
..,--------,*/
To learn how the code works I highly recommend checking out the author's explanation: https://www.a1k0n.net/2011/07/20/donut-math.html
The transition to "Churro.c"
I initially came across the code on a Joma Tech video. It seemed like an interesting project to undertake, but I eventually forgot about it. Until it made news in my country. At that point I made sure that at some point in the near future I had to understand how this spinning doughnut worked.
The best way that I've found to learn something, is to work with it myself. Thereafter I wanted to make my own version of the doughnut, but with something that resonates better with what we have in my country. Since doughnuts are not very popular, I went for a very similar alternative, churros.
There are two things to note about Donut.c:- Its toroidal structure: Thanks to this structure, the code is easier on the eyes, as calculus of luminosity at each point is simple.
- Its terminal output: Although its terminal output looks awesome, there can't be too much detail on the object. Since a churro has much more detail, another method for visualization must be used.
To solve the lack of detail with the terminal output, I relied on Processing. It enabled me to easily replicate the original output from the Donut.c author:

To adapt the code to make a churro, there were two steps to be performed:
- Change the rotated area: In the Donut.c code, a circle is rotated around the y axis to give the illusion of a doughnut. In my case it had to be a something more like a star.
- Adapt the luminosity: Since it's not a circle anymore, there are more changes in lighting in each rotation.
Changing the rotated area
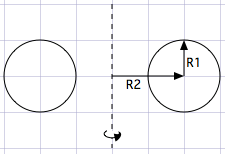
Regarding the original code, R2 does not need to be changed. However, R1 will need to change depending on the angle. I have adapted it so that it follows the function:
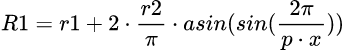
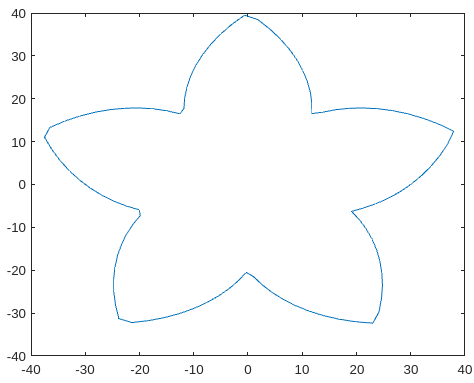
This results in the following section (which is later shifted along the x axis because of R2's effect):
Computing the new illumination
Initially I made an attempt at computing the exact normal vector that the Churro should have at each point. However, as equations started to become bigger and bigger, I chose to simplify the shape. By choosing to work with a star-like shape, the normal at each point can be computed much easily:
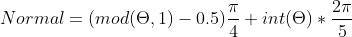
Resulting output
Lastly, I checked that the illumination was set properly by plotting the circular version of the Churro. Since it looked similar than the resulting illumination on the doughnut, but with the small adaptations made for the star-like pattern, I considered the project a success.
For the final version, a distortion was performed on one of the axis, and the rotation along the y axis was shortened, to give it a more churro-like appearance.


Thanks for reading, here's a chocolate churro.

